| Autore |
 Discussione  |
|
giuliof
Utente V.I.P.
Città: Torino
Prov.: Torino
Regione: Piemonte
291 Messaggi
Tutti i Forum |
|
|
a p
utente ritirato in data 22.02.2012
9799 Messaggi
|
 Inserito il - 31 luglio 2007 : 12:15:32
|
Dicono che si veda dal Monte Baldo (VR)
 Alessandro PD
Chi ama la Natura le lascia i suoi fiori |
 |
|
|
Stekal
Moderatore
Città: CANTU'
Prov.: Como
Regione: Lombardia
4435 Messaggi
Fotografia Naturalistica |
Inserito il - 31 luglio 2007 : 13:33:06
Nazione: Italia Regione: Lombardia Provincia: CO Comune: Lanzo Intelvi Localitŕ:Sighignola
|
Se vuoi te lo mostro dalla cima del Monte Sighignola (ho messo la localizzazione in modo che puoi visualizzare dov'è con google map):
probabilmente ho in giro qualcos'altro da altre cime (Resegone ad esempio, ma non cambia molto).. purtroppo più si va verso le Alpi più settentrionali più è difficile vederlo (ostruito dai monti davanti) a meno che non si salga proprio sulle cime più alte, ma per adesso non ho foto..
Stefano |
Modificato da - Stekal in data 31 luglio 2007 19:00:55 |
|
|
|
Stekal
Moderatore
Città: CANTU'
Prov.: Como
Regione: Lombardia
4435 Messaggi
Fotografia Naturalistica |
Inserito il - 31 luglio 2007 : 19:25:26
|
| | Ma il Monviso fino dove e' possibile vederlo |
Interessa anche una risposta "kilometrica" da geom-ing?  
Stefano |
|
|
|
Alberto Gozzi
Moderatore
Città: Trento
Prov.: Trento
Regione: Trentino - Alto Adige
26216 Messaggi
Tutti i Forum |
Inserito il - 01 agosto 2007 : 00:11:41
|
ceeeerto che sì, Stefano !!!!! 
...questo vale solo per me...
dal Trentino credo di non averlo mai visto (neanche con il binocolo  )!!!!
un saluto a tutti..........alberto
|
Modificato da - Alberto Gozzi in data 01 agosto 2007 00:14:22 |
|
|
|
giuliof
Utente V.I.P.
Città: Torino
Prov.: Torino
Regione: Piemonte
291 Messaggi
Tutti i Forum |
Inserito il - 01 agosto 2007 : 10:46:44
|
Benvenga qualsiasi tipo di risposta, anche per "sentito dire" ...
Qui dalle mie parti si dice che dalle Dames de Challand, dalla capanna Margerita,
e ... perfino dal Mombarone ... in certe condizioni si vede anche il mare ...
gf |
|
|
|
Carlmor
Moderatore Trasversale
Città: Varese
Prov.: Varese
Regione: Lombardia
8940 Messaggi
Flora e Fauna |
Inserito il - 01 agosto 2007 : 12:35:16
|
Dalle prealpi varesine meridionali si vede bene, ma questo probabilmente era prevedibile
Carlo
|
|
|
|
Carlao
Utente V.I.P.
Città: Vimercate (MB)
Prov.: Milano
Regione: Lombardia
268 Messaggi
Fotografia Naturalistica |
Inserito il - 01 agosto 2007 : 14:29:37
|
| non ho prove fotografiche, ma ricordo di aver visto il Monviso dalla Grigna e dal Resegone... |
|
|
|
Stekal
Moderatore
Città: CANTU'
Prov.: Como
Regione: Lombardia
4435 Messaggi
Fotografia Naturalistica |
Inserito il - 01 agosto 2007 : 19:21:26
|
Ok, ve la siete cercata, eh!
Quello che cerchiamo di fare è di stabilire il limite geometrico oltre il quale sarebbe impossibile vedere il Monviso.. il limite è ovviamente dovuto al fatto che la terra è sferica (o grossomodo) e che quindi ad una certa distanza la montagna scomparirebbe sotto la linea dell'orizzonte.
In questo calcolo facciamo alcune ipotesi:
1- approssimiamo la terra come sferica;
2- non consideriamo la presenza dell'atmosfera, ovvero la foschia, la rifrazione, etc..
3- non consideriamo la presenza di occlusioni, come montagne e colline tra noi e il Monviso..
detto questo, lo schema può essere il seguente:
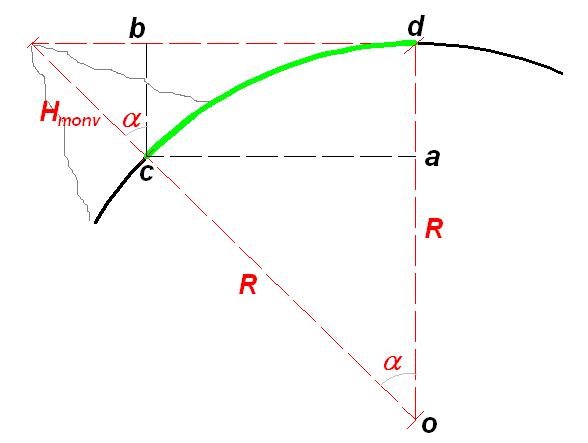
in nero la superficie terrestre, sulla sinistra il Monviso, il punto o è il centro della terra, R il raggio terrestre, d è il punto dell'osservatore oltre il quale non è più possibile osservare la punta del monte, alfa è l'angolo al centro tra il Monviso e l'osservatore.. Il tratto in verde (cd) è la distanza che ci interessa.
Con una semplice relazione geometrica possiamo scrivere:
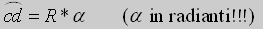
quindi, conoscendo R, per applicare la formula dobbiamo calcolare l'angolo alfa.
Sempre geometricamente, guardando la figura, possiamo scrivere R come la somma di due contributi, (oa) + (ad), ma (ad) è anche uguale a (cb), quindi, ricordando le formule base di trigonometria:
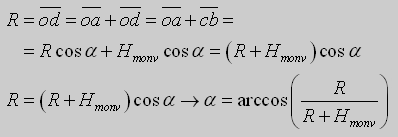
cioè, sostituendo i valori reali si ottiene:
ovvero, secondo le ipotesi sopra, la distanza massima di un osservatore (che si trova sulla sfera che approssima la terra (cioè a livello del mare!)) dal Monviso per riuscire a vedere il monte è di 221km circa..
|
|
|
|
Stekal
Moderatore
Città: CANTU'
Prov.: Como
Regione: Lombardia
4435 Messaggi
Fotografia Naturalistica |
Inserito il - 01 agosto 2007 : 19:21:36
|
Più interessante è un altro ragionamento: se guardiamo il monte da una zona che non sia il livello del mare ma dalla pianura o da un monte ci troviamo più in quota; ad intuito vediamo che più ci spostiamo in quota più la distanza massima deve aumentare. Anche qui uno schema:
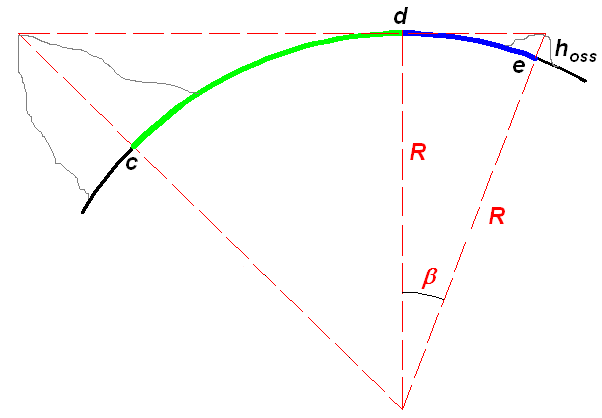
Se l'osservatore si trova sulla collinetta/montagna di destra la distanza massima è più lunga di quella relativa alla linea dell'orizzonte dal Monviso. In questo caso più generale la distanza di interesse è data dalla somma del tratto verde e del tratto blu. Il tratto verde è lo stesso calcolato prima, il tratto blu si calcola esattamente nello stesso modo, sostituendo alla quota del Monviso la quota dell'osservatore..
ad esempio se ipotizziamo di essere a 1000 metri di quota:
cioè, salendo in quota di 1000 m, la distanza massima aumenta da 221 km a 333 km!
Proviamo a giocare con le quote:
Quota ---> distanza massima
----------------------------
0000 m -------> 221 km
0500 m -------> 300 km
1000 m -------> 333 km
1500 m -------> 359 km
2000 m -------> 381 km
2500 m -------> 399 km
3000 m -------> 416 km
che, riportati su una mappa, ci danno il limite geometrico della visibilità:
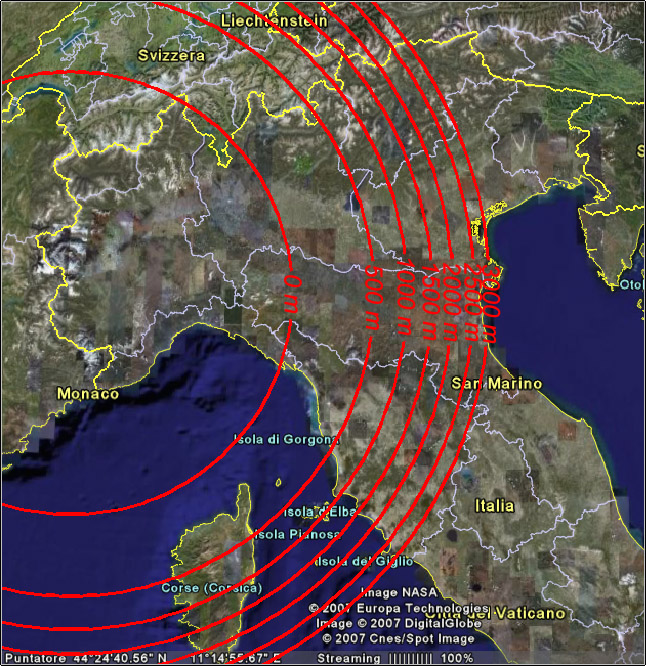
282,7 KB
ad esempio, se fossimo sul delta del Po, per vedere il Monviso dovremmo salire sopra i 3000m
Chiedo scusa se ho affrontato argomenti banali o complicati (a seconda del caso, lungi da me passare per geometra o ingegnere, sono formule da terza superiore!) in maniera sbagliata o in modo non chiaro, ma proprio non avevo idea di come fare
PS: spero non abbia fatto errori altrimenti...  .. se ci sono ditemelo!!
Stefano |
|
|
|
Carlmor
Moderatore Trasversale
Città: Varese
Prov.: Varese
Regione: Lombardia
8940 Messaggi
Flora e Fauna |
Inserito il - 01 agosto 2007 : 19:56:49
|
Stefano, cominci a farmi un po' paura 
comunque grazie per aver chiarito l'argomento in modo così dettagliato ..
Carlo
|
|
|
|
FOX
Moderatore
Città: BAGNO A RIPOLI
Regione: Toscana
21536 Messaggi
Tutti i Forum |
Inserito il - 01 agosto 2007 : 20:11:29
|
Grazie Ste,
ora abbiamo un pò di più le idee chiare...
simo
Alto è il prezzo quando si sfida per vanità il mistero della Natura - I. Sheehan |
|
|
|
Alberto Gozzi
Moderatore
Città: Trento
Prov.: Trento
Regione: Trentino - Alto Adige
26216 Messaggi
Tutti i Forum |
Inserito il - 01 agosto 2007 : 20:36:26
|
adesso avete capito perchè è diventato moderatore
..........alberto
grazie,Stefano  |
|
|
|
bepilovato
Utente V.I.P.
Città: bolzano
Prov.: Bolzano
Regione: Trentino - Alto Adige
494 Messaggi
Tutti i Forum |
Inserito il - 01 agosto 2007 : 22:14:40
|
Accidenti Stekal, ma posso chiederti chi sei?? cioè che studio hai? veramente fai paura!!
Bando agli scherzi, complimenti, perchè una volta con i miei colleghi si parlava che cima fosse quel dentino visto con il binocolo, io ho sparato che dalla forma poteva essere il Monviso, nò è troppo lontano il Monviso.. al momento ho pensato che era vero, adesso non ne sono più tanto sicuro, penso che allora avevo ragione.... la cima in questione se non sbaglio e se non ricordo male era il Gran Pilastro dopo un temporale, con l'atmosfera pulitissima. E il Gran Pilastro ha una quota di 3510m. ed è abbastanza isolato da avere un panorama grandioso..
ogni modo ciao bepi
bepilovato |
|
|
|
Istrice
Amministratore
Città: Ostia
Prov.: Roma
Regione: Lazio
10849 Messaggi
Tutti i Forum |
Inserito il - 01 agosto 2007 : 22:22:30
|
Stekal...sei perfetto!!!
da buon matematico mi ha colpito molto il tuo approccio..bravissimo! |
|
|
|
giuliof
Utente V.I.P.
Città: Torino
Prov.: Torino
Regione: Piemonte
291 Messaggi
Tutti i Forum |
Inserito il - 02 agosto 2007 : 14:01:41
|
Grande Stekal... !!!!
gf
|
Modificato da - giuliof in data 02 agosto 2007 14:02:04 |
|
|
|
ametista
Moderatore
 di imagesCA457P3I.jpg)
Prov.: Padova
Regione: Veneto
6209 Messaggi
Flora e Fauna |
Inserito il - 02 agosto 2007 : 15:05:50
|
| | ... sono formule da terza superiore! |
o quarta :)
stefano ho urgente bisogno di ripetizioni di goniometria e trigonometria!!!!
...saresti un ottimo prof!! 
|
|
|
|
corto_circuito
Utente Junior
Città: Cabiate
Prov.: Como
Regione: Lombardia
82 Messaggi
Fotografia Naturalistica |
Inserito il - 02 agosto 2007 : 15:19:07
|
grande stekal!! avrei bisogno anche io un po' di ripasso, non ti arrabbi vero se ti frego le formule già pronte...lol
La vita è come la scala del pollaio: corta ripida e piena di m...a |
|
|
|
Bigeye
Moderatore
Città: viterbo
Prov.: Viterbo
Regione: Lazio
6269 Messaggi
Flora e Fauna |
Inserito il - 03 agosto 2007 : 10:21:29
|
eppure mi sembrava un ragazzo normale.....
:)
okkione |
|
|
|
a p
utente ritirato in data 22.02.2012
9799 Messaggi
|
Inserito il - 03 agosto 2007 : 12:39:36
|
per un po' di formule di trigonometria
Alessandro PD
Chi ama la Natura le lascia i suoi fiori |
|
|
|
Stekal
Moderatore
Città: CANTU'
Prov.: Como
Regione: Lombardia
4435 Messaggi
Fotografia Naturalistica |
Inserito il - 04 agosto 2007 : 21:19:39
|
Grazie a tutti ! ma come dice giustamente Alessandro, in fondo sono 2 formule di trigonometria..
| Messaggio originario di bepilovato:
Accidenti Stekal, ma posso chiederti chi sei?? cioè che studio hai? veramente fai paura!!
Bando agli scherzi, complimenti, perchè una volta con i miei colleghi si parlava che cima fosse quel dentino visto con il binocolo, io ho sparato che dalla forma poteva essere il Monviso, nò è troppo lontano il Monviso.. al momento ho pensato che era vero, adesso non ne sono più tanto sicuro, penso che allora avevo ragione.... la cima in questione se non sbaglio e se non ricordo male era il Gran Pilastro dopo un temporale, con l'atmosfera pulitissima. E il Gran Pilastro ha una quota di 3510m. ed è abbastanza isolato da avere un panorama grandioso..
|
In realtà.. sono davvero geometra! Poi ho anche "approfondito" ed ora (da dottorando) mi occupo della misura della terra dallo spazio (GPS)..
Mi fa molto piacere, se era lui sarebbe una specie di conferma... cavolo, oltre 400 km di visibilità!
| Messaggio originario di ametista:
stefano ho urgente bisogno di ripetizioni di goniometria e trigonometria!!!!
|
Quando vuoi!!
| Messaggio originario di corto_circuito:
grande stekal!! avrei bisogno anche io un po' di ripasso, non ti arrabbi vero se ti frego le formule già pronte...lol
|
Certo che no!!! Ma a cosa ti servono!!???!
Stefano |
|
|
|
Discussione |
|
Forum
|
Registrati
|
Msg attivi
|
Msg Recenti
|
Msg Pvt
|
Utenti
|
Galleria |
Map |
Gadgets
|
Cerca
|
|
FAQ | Regole |
| 
| 
Suggerimento: Hai provato la nostra ricerca tassonomica da Browser? Clicca qui per info!
Ma il Monviso fino dove e' possibile vederlo ?
