| Autore |
 Discussione  |
|
marz
Utente Super
Città: Bergamo
Regione: Lombardia
8788 Messaggi
Tutti i Forum |
|
|
CIACCA
Utente Senior
Città: Longarone
Prov.: Belluno
Regione: Veneto
1495 Messaggi
Tutti i Forum |
 Inserito il - 13 gennaio 2010 : 23:17:08
|
Premetto che non sono un'esperto.
Comunque credo che oltre ad un limite dovuto all'altezza dei punti ci sia da considerare anche la rifrazione della luce attraverso l'aria, che può distorcere un po' la linearità.
Mi fermo qui per non dire bestialità.
Sarei curioso anch'io di conoscere il fenomeno in maniera più approfondita da un punto di vista fisico.
Ciao Christian |
 |
|
|
gabrielebesostri2
Utente Senior
Città: Torre d'Arese
Prov.: Pavia
Regione: Lombardia
894 Messaggi
Tutti i Forum |
Inserito il - 14 gennaio 2010 : 00:53:39
|
Buonasera
mi permetto di indicare i due calcoli (fra monte/orizzonte a quota zero e monte/monte) senza tenere conto della rifrazione atmosferica
monte/orizzonte quota zero
d=distanza orizzonte da calcolare
h=altezza monte
r= raggio terrestre (6377 medio)
d=radice quadrata di h*h + 2*r*h
in pratica se fossi sul monte penice (h=1,460km) otterrei
d=radice quadrata di 1,460*1,460 + 2*6377*1,460 = 136.47km all' orizzonte
se fossi in piedi sulla spiaggia a quota zero otterrei
h=1.75m altezza miei occhi (0.00175km)
r= raggio terrestre (6377 medio)
d orizzonte=radice quadrata di 0.00175*0.00175 + 2*6377*0.00175= 4.72km all' orizzonte
monte/monte se visibili o no fra di loro
d1=orizzonte monte A
d2=orizzonte monte B
h1=quota monte A
h2=quota monte B
D=distanza nota fra i due monti
r=raggio terrestre (6377 km medio)
se la somma di d1+d2 è > di D i monti si "vedono" altrimenti no, formuletta
d1+d2= [radice quadrata di (h1*h1 + 2*r*h1)] + [radice quadrata di (h2*h2 + 2*r*h2)] se > di D i monti si "vedono"
esempio.
Monte Penice h1=1,460km
Monte Rosa h2=4,633km
D nota fra i due monti 171 km
r=6377km
otteniamo
[radice quadrata di (1,460*1,460 + 2*6377*1.460)] + [radice quadrata di (4,633*4,633 + 2*6377*4,633)]= 136.458 + 243.08= 379.54km > 171... i monti si "vedono"
altro esempio
Etna h1=3,323km
Monte Rosa h2=4.633km
D nota fra i due monti 1082 km
r=6377km
[radice quadrata di (3,323*3,323 + 2*6377*3,323)] + [radice quadrata di (4,633*4,633 + 2*6377*4,633)]= 205.87 + 243.08= 448.94km < 1082... i monti non si "vedono"
è tardi, buonanotte... spero mi perdoniate eventuali errori...
Lele
Link
Quando avrete abbattuto l'ultimo albero, quando avrete pescato l'ultimo pesce, quando avrete inquinato l'ultimo fiume, allora vi accorgerete che non si può mangiare il denaro (proverbio indiano) |
|
|
|
gabrielebesostri2
Utente Senior
Città: Torre d'Arese
Prov.: Pavia
Regione: Lombardia
894 Messaggi
Tutti i Forum |
Inserito il - 14 gennaio 2010 : 08:54:01
|
Buongiorno
...chiaramente gli errori di rifrazione atmosferica (tanto a me cari quando lavoro, comunque compensati dalle strumentazioni elettroniche oggi in normale uso)incidono abbastanza su misure "precise" (tracciamenti di vaste estensioni di terreno, picchettamenti stradali e ferroviari ecc.)
in ogni caso, allego la formula, presa da un mio testo di topografia...
per provare, il consiglio è quello di cimentarsi su misure "grandi".
Questa formula serve per compensare la distanza "misurata" ma può essere usata anche in maniera inversa per misure dell' orizzonte
Immagine:
290,11 KB
Link
Quando avrete abbattuto l'ultimo albero, quando avrete pescato l'ultimo pesce, quando avrete inquinato l'ultimo fiume, allora vi accorgerete che non si può mangiare il denaro (proverbio indiano) |
|
|
|
leonella55edo47
Utente Super
5652 Messaggi
Tutti i Forum |
Inserito il - 14 gennaio 2010 : 19:19:53
|
Frugando nei nostri archivi abbiamo trovato questa vecchia fotografia di Edo, subito dopo la Creazione, cui appare in sogno la soluzione del problema.
In aggiunta, una tabellina con a sinistra l'altezza in metri del monte, a destra la distanza in km dell'orizzonte.
Speriamo vi piaccia...  
|
|
|
|
gabrielebesostri2
Utente Senior
Città: Torre d'Arese
Prov.: Pavia
Regione: Lombardia
894 Messaggi
Tutti i Forum |
Inserito il - 14 gennaio 2010 : 19:42:03
|
Edo, attento! Quando Archimede intimò al soldato romano il "NOLI TANGETE..." venne subito dopo pugnalato!!!
(però da quanto vedo tu non sei sulla spiaggia di Siracusa ove accadde il fatto...)
Lele
Link
Quando avrete abbattuto l'ultimo albero, quando avrete pescato l'ultimo pesce, quando avrete inquinato l'ultimo fiume, allora vi accorgerete che non si può mangiare il denaro (proverbio indiano) |
|
|
|
Stekal
Moderatore
Città: CANTU'
Prov.: Como
Regione: Lombardia
4435 Messaggi
Fotografia Naturalistica |
Inserito il - 14 gennaio 2010 : 20:25:47
|
Ne avevo parlato qui, ma io avevo usato gli angoli
Link
Stefano |
|
|
|
leonella55edo47
Utente Super
5652 Messaggi
Tutti i Forum |
Inserito il - 14 gennaio 2010 : 20:52:53
|
Ciao, Stefano.
La tabellina risolve anche la questione se il Bianco sia visibile dal Guglielmo o meno, per la presenza del Corno Bianco.
Con facili passaggi e divertente ginnastica, si dovrebbe concludere che proprio non si vede, perchè (con quelle altezza) il limite dovrebbe essere a circa 75km, e quella è proprio la distanza del Corno Bianco.
Devo ancora tornare sul Guglielmo per controllare de visu.
A Lele: Archimede fu colpito a morte perchè il sodato romano capì: Noli frangere circulos meos, ed equivocò. Ma voi siete persone di cultura, e poi è tutto scritto...
Edo |
|
|
|
Stekal
Moderatore
Città: CANTU'
Prov.: Como
Regione: Lombardia
4435 Messaggi
Fotografia Naturalistica |
Inserito il - 14 gennaio 2010 : 21:06:51
|
Ecco la simulazione (assolutamente affidabile) del panorama dal Monte Guglielmo (fatta con il solito sito Link
Immagine:
96,58 KB
Stefano |
|
|
|
Stekal
Moderatore
Città: CANTU'
Prov.: Como
Regione: Lombardia
4435 Messaggi
Fotografia Naturalistica |
Inserito il - 14 gennaio 2010 : 21:17:58
|
Si può fare il giochino contrario e vedere che 'nostre' montagne si vedono dal Bianco:
Immagine:
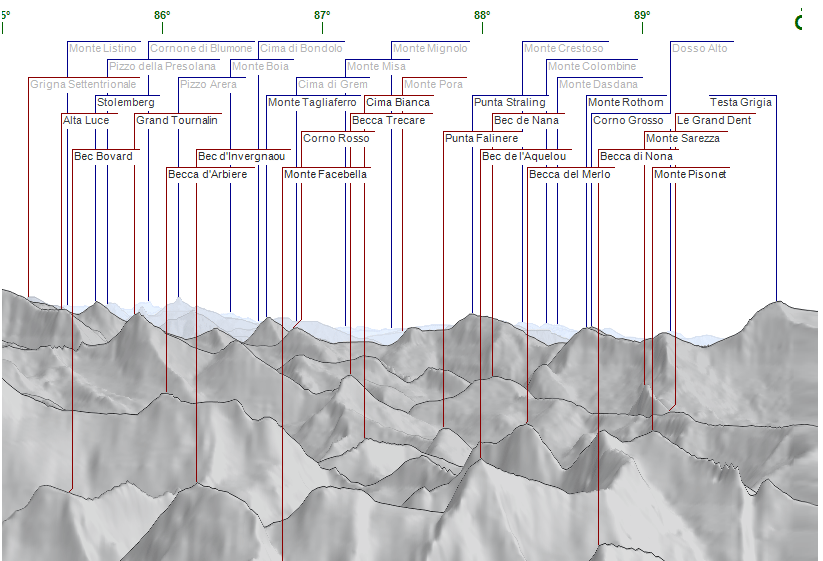
129,78 KB
dalla Grignetta (non segnata ma è la montagna appena davanti al Pizzo Arera) io l'ho visto una volta. Uno dei punti migliori sembra essere proprio il Pizzo Arera, da cui si vede così:
Immagine:
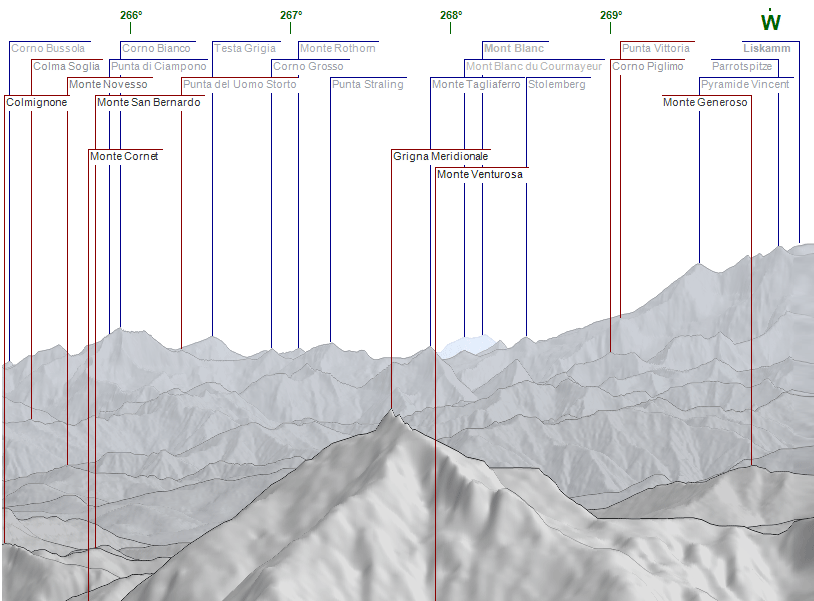
137,16 KB
..un pensierino..
fine off-topic
Stefano |
|
|
|
marz
Utente Super
Città: Bergamo
Regione: Lombardia
8788 Messaggi
Tutti i Forum |
Inserito il - 14 gennaio 2010 : 22:58:49
|
Ringrazio le migliori menti del forum per le risposte, celeri e precise.
Mi scuso con Stefano perchè non ricordavo più quella discussione che ha richiamato (e cui avevo anche partecipato ) e raccolgo senz' altro il suggerimento per l' Arera che quest' anno conto assolutamente di fare.
Vorrei però cercare di far capire i concetti sin qui espressi alla "casalinga di Voghera" (quando io ero parecchio più giovane la "Casalinga di Voghera" era un'espressione molto comune nel lessico giornalistico, con cui si intendeva rappresentare quella fascia della popolazione italiana dal non particolarmente elevato livello di istruzione).
Credo che la tabella di Edo sia sufficientemente chiara anche per la casalinga di Voghera (del resto era stato ispirato...).
Se riuscissimo ad affiancare a quella tabella un' altra semplice semplice con cui facciamo capire come la stessa si modifica al crescere dell' altezza del punto di osservazione credo che faremmo (o, per meglio dire, fareste) una cosa utile.
marz |
Modificato da - marz in data 14 gennaio 2010 23:00:43 |
|
|
|
Stekal
Moderatore
Città: CANTU'
Prov.: Como
Regione: Lombardia
4435 Messaggi
Fotografia Naturalistica |
Inserito il - 14 gennaio 2010 : 23:34:32
|
Ci ho provato:
Immagine:
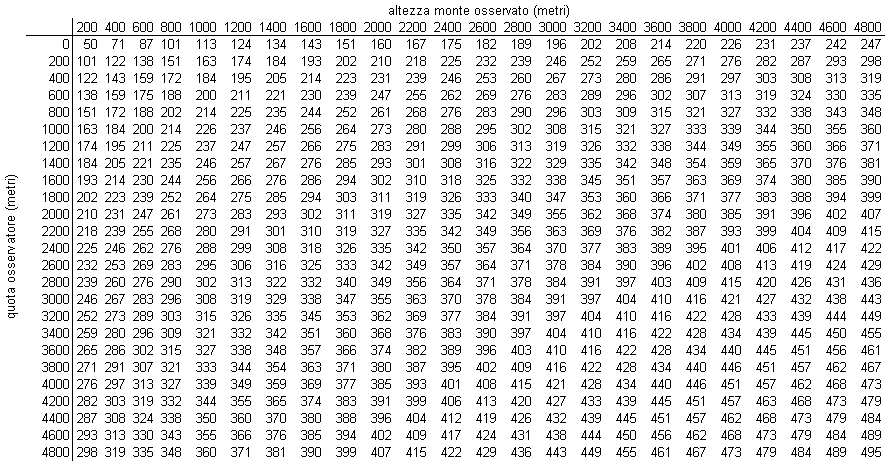
15,63 KB
la distanza è in km, ed è la distanza massima cui la montagna deve trovarsi dall'osservatore per essere visibile
inoltre allego uno stupidissimo foglio Excel dove si possono mettere i valori di quota dell'osservatore e dell'altezza del monte che si vuole osservare: la distanza viene calcolata in automatico
Link
fatemi sapere se trovate errori, ma i risultati mi tornano con quelli di Edo
Stefano |
|
|
|
marz
Utente Super
Città: Bergamo
Regione: Lombardia
8788 Messaggi
Tutti i Forum |
Inserito il - 14 gennaio 2010 : 23:43:03
|
Magnifico, Stefano.
Per quella che è la mia esperienza, torna tutto.
marz |
|
|
|
virtuafiume
Utente Junior
Città: montanaro
Prov.: Torino
Regione: Piemonte
83 Messaggi
Fotografia Naturalistica |
Inserito il - 16 gennaio 2010 : 11:09:26
|
Buongiorno,
Come sempre ho trovato questa pagina molto interessante e il file excel ci risolve tutti i problemi dovuti a questo fatto.
Ma non siamo gli unici ad aver avuto questo "problema".
Alcuni nostri colleghi francesi combattono con i calcoli della curvatura terrestre e sopratutto sulle valutazioni relative alla rifrazione dell'aria studiando il fenomeno della COrsica vista dalla Costa Azzurra.
Vi posto il link a un sito che inquadra il problema in termini diciamo scientifici, come si vede dalle immagini in questo caso siamo proprio ai limiti dei calcoli di curvatura terrestre e si sperimenta l'incidenza della rifrazione dovuta all'acqua del mare e all'aria.
Link
In più un'immagine tratta da questo sito (Link) sulla Corsica vista dal Mercantour!!!
Immagine:
133,28 KB
PS - A proposito di Corsica, appena la trovo vi linko una foto di uno scalatore del Monviso che ha fotografato l'Ile de Beauté dai 3841 m del Viso!!! Secondo il mitico sito di Ulrich Deuschle questo è possibile
Andrea |
|
|
|
Albisn
Utente Senior
Città: Seregno
Prov.: Milano
Regione: Lombardia
4311 Messaggi
Flora e Fauna |
Inserito il - 17 gennaio 2010 : 16:59:58
|
Bellissima questa discussione|
Ho iniziato a leggerla con una certa sufficienza. Ho qualche reminiscenza di trigonometria...
Cammin facendo mi sono sorti alcuni dubbi, ma ora non ho proprio tempo...
Alla fine comunque mi sento io il "Casalingo di Voghera" (con la C maiuscola però per evitare eccessivo autolesionismo). Ma un giorno o l'altro mi metto a schiacciare bottoni su Excel, o meglio ancora su Calc (il regolo non so dove è finito) e vi farò vedere...
A parte gli scherzi per dirvi: Bravi tutti, complimenti e continuate!
Fantastiche le foto e i disegni... ma dove accidenti siete andati a scovarli? (domanda retorica solo per ribadire che siete bravi). Mi torna persino la voglia di andare sul Pizzo Arera... e di andare a controllare la faccenda di Archimede.
Saluti
Alberto
|
Modificato da - Albisn in data 17 gennaio 2010 17:02:02 |
|
|
|
Geom
Utente Senior
Città: Piacenza
Prov.: Piacenza
Regione: Emilia Romagna
510 Messaggi
Tutti i Forum |
Inserito il - 05 marzo 2010 : 17:38:18
|
Concordo, bellissima discussione!
io utilizzo un altro metodo, forse un po' più semplice.
sul formulario dell' IGM (istituto geografico militare) c'è una piccola e semplice tabella:
Immagine:
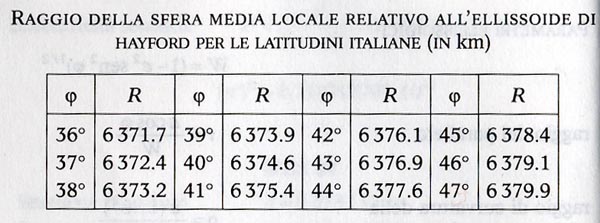
56,83 KB
i gradi sono la latitudine, mentre R sta per Raggio Terrestre.
detto cio:
se si fa una media fra i raggi delle latitudini interessate, si trova il raggio!
con AutoCAD si disegna un cerchio di quelle dimensioni e poi partendo dal centro si fa una linea che incontri la circonferenza (un raggio)
Fatto questo la si estende in base all'altezza del Monte da dove partiamo (attenzione alle unità di misura: è tutto in Km)
Poi si fa una linea che parte dalla "punta del monte" tangente alla circonferenza.
adesso la estediamo un po' (tipo di 500Km)
poi si fa un cerchio (con TangTangRaggio) mettiamo di raggio 2km [valido per una montagna alta 4km].
si va a vedere dov'è stato disegnato il cerchio e da li calcoleremo la distanza dal nostro monte di partenza: abbiamo trovato la distanza massima a cui potremmo vedere un monte alto 4km.
spero di essere stato chiaro, comunque è più facile da fare che da spiegare (per chi sa usare un po' AutoCAD)
Luca  |
|
|
|
macromicro
Utente Super
Città: Piovene Rocchette
Prov.: Vicenza
Regione: Veneto
7113 Messaggi
Macrofotografia |
Inserito il - 07 marzo 2010 : 08:55:23
|
Che bello ed interessante vedere le immagini/nomi dei monti come riportato nei messaggi del 14/01 di Stekal
Gianfranco |
|
|
|
marz
Utente Super
Città: Bergamo
Regione: Lombardia
8788 Messaggi
Tutti i Forum |
Inserito il - 20 dicembre 2011 : 22:25:39
|
Riprendo questa vecchia discussione, perchè sono in grado di farvi vedere la Corsica fotografata dall' Italia, dalla zona delle Cinque Terre, in Liguria.
Il Monte Cinto, 2706 metri è la vetta più elevata della Corsica.
cliccare sulla foto
280,51 KB
Giuseppe |
|
|
|
marco cant
Utente Senior
Città: Montignoso
Prov.: Massa Carrara
Regione: Toscana
849 Messaggi
Tutti i Forum |
Inserito il - 21 dicembre 2011 : 14:55:36
|
Ottimo lavoro Giuseppe, per me è un piacere vedere i nomi dei monti corsi, fra l'altro si tratta più o meno della prospettiva che alcune volte riesco a vedere da casa mia.
Marco
------------------
Salviamo le Apuane
------------------ |
|
|
|
FOX
Moderatore
Città: BAGNO A RIPOLI
Regione: Toscana
21536 Messaggi
Tutti i Forum |
Inserito il - 21 dicembre 2011 : 15:28:18
|
| Messaggio originario di marz:
Riprendo questa vecchia discussione, perchè sono in grado di farvi vedere la Corsica fotografata dall' Italia, dalla zona delle Cinque Terre, in Liguria.
Il Monte Cinto, 2706 metri è la vetta più elevata della Corsica.
cliccare sulla foto
280,51 KB
Giuseppe
|
WOWOWWWW...
Osservo con molto piacere!!!
Grazie Marz...bravo!!!
simo
Osserva in profondità, nel profondo della natura, solo così potrai comprendere ogni cosa. - Albert Einstein |
|
|
|
marco cant
Utente Senior
Città: Montignoso
Prov.: Massa Carrara
Regione: Toscana
849 Messaggi
Tutti i Forum |
Inserito il - 12 gennaio 2012 : 09:01:09
|
A proposito di visibilità delle montagne vorrei sottoporvi alcune foto scattate a dicembre del 2011 dalla spiaggia di Marina di Massa (44°00' N - 10° 06'W) guardando verso SSW dove generalmente si può scorgere la sagoma della Corsica si vedevano delle sagome diverse dal solito. E' successo per due sere consecutivamente, vi allego delle foto effettuate in discoping, non sono riuscito a spiegarmi il fenemone, fra l'altro nella terza sembrerebbe esserci la sagoma di un faro? Cosa ne pensate? Fenomeno ottico o semplicemnte una particolare visibilità che che elimenava del tutto gran parte delle montagne normalmente visibili?
Marco
Immagine:
185,9 KB
Immagine:
106,49 KB
------------------
Salviamo le Apuane
------------------ |
|
|
|
Discussione |
|
Forum
|
Registrati
|
Msg attivi
|
Msg Recenti
|
Msg Pvt
|
Utenti
|
Galleria |
Map |
Gadgets
|
Cerca
|
|
FAQ | Regole |
| 
| 
Suggerimento: Leggi il nostro regolamento!! Clicca qui!
Curvatura terrestre e visibilità dai monti
